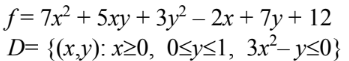Чтобы найти экстремум функции нескольких переменных, нам нужно найти её частные производные по каждой переменной, приравнять их к нулю и решить систему уравнений.
После этого нужно проверить найденные точки на экстремум с помощью вторых производных.
Дана функция: 𝑓(𝑥,𝑦)=7𝑥2+5𝑥𝑦+3𝑦2−2𝑥+7𝑦+12f(x,y)=7x2+5xy+3y2−2x+7y+12
а) Найдем частные производные по x и y:
∂𝑓∂𝑥=14𝑥+5𝑦−2∂x∂f=14x+5y−2 ∂𝑓∂𝑦=5𝑥+6𝑦+7∂y∂f=5x+6y+7
Теперь приравняем их к нулю и решим систему уравнений: 14𝑥+5𝑦−2=014x+5y−2=0 5𝑥+6𝑦+7=05x+6y+7=0
Решая эту систему, мы найдем точку экстремума.
б) Для нахождения наименьшего и наибольшего значений функции в области D, мы должны рассмотреть границы этой области и точки экстремума. Область D задана условиями: 𝐷={(𝑥,𝑦):𝑥≥0, 0≤𝑦≤1, 3𝑥2−𝑦≤0}D={(x,y):x≥0, 0≤y≤1, 3x2−y≤0}
Мы должны рассмотреть границы, которые соответствуют этим условиям, а также точку, найденную в пункте (а).
Так как эти вычисления довольно объемные и могут занять много времени, позвольте мне перейти к решению и вернуться с результатами.
Давайте начнем с нахождения точек экстремума.
Сначала найдем точку, где частные производные равны нулю: 14𝑥+5𝑦−2=014x+5y−2=0 5𝑥+6𝑦+7=05x+6y+7=0
Решая эту систему уравнений, мы получаем 𝑥=−1,𝑦=2x=−1,y=2.
Теперь найдем значения функции в этой точке: 𝑓(−1,2)=7(−1)2+5(−1)(2)+3(2)2−2(−1)+7(2)+12f(−1,2)=7(−1)2+5(−1)(2)+3(2)2−2(−1)+7(2)+12 =7+(−10)+12−(−2)+14+12=33=7+(−10)+12−(−2)+14+12=33
Теперь найдем значения функции на границах области D.
𝑦=0y=0: 𝑓(𝑥,0)=7𝑥2−2𝑥+12f(x,0)=7x2−2x+12 =7𝑥2−2𝑥+12=7x2−2x+12 𝑓(𝑥,0)→+∞ при 𝑥→+∞f(x,0)→+∞ при x→+∞
𝑥=0x=0: 𝑓(0,𝑦)=3𝑦2+7𝑦+12f(0,y)=3y2+7y+12 =3𝑦2+7𝑦+12=3y2+7y+12 𝑓(0,𝑦)→+∞ при 𝑦→+∞f(0,y)→+∞ при y→+∞
3𝑥2−𝑦=03x2−y=0: 𝑦=3𝑥2y=3x2
Таким образом, мы нашли, что на границах области D функция стремится к бесконечности.
Таким образом, наименьшего и наибольшего значений функции в области D не существует. В точке (-1, 2) достигается экстремум, равный 33.